Show List
Congruence
Discover the concept of congruence with our interactive guide designed for grade 4-6 kids.
In mathematics, congruence refers to the relationship between two figures or shapes that are identical in size and shape, but may not necessarily be in the same position. Two figures are considered congruent if they can be superimposed on one another exactly, or if one can be obtained from the other by a combination of translation, rotation and reflection.
Congruence can be represented using the symbol '≅', for example:
Triangle ABC ≅ Triangle DEF
This means that triangle ABC is congruent to triangle DEF.
In Geometry, we can use congruence to prove that two figures are the same. For example, if we can prove that two triangles are congruent, we know that they have the same size and shape, and that corresponding angles and sides are equal.
There are different ways to prove that two figures are congruent, such as:
- SAS congruence: two figures are congruent if we can prove that two pairs of sides and the included angle are equal.
- SSS congruence: two figures are congruent if we can prove that all three pairs of sides are equal.
- ASA congruence: two figures are congruent if we can prove that two pairs of angles and one pair of sides are equal.
- AAS congruence: two figures are congruent if we can prove that two pairs of angles and a non-included side are equal.

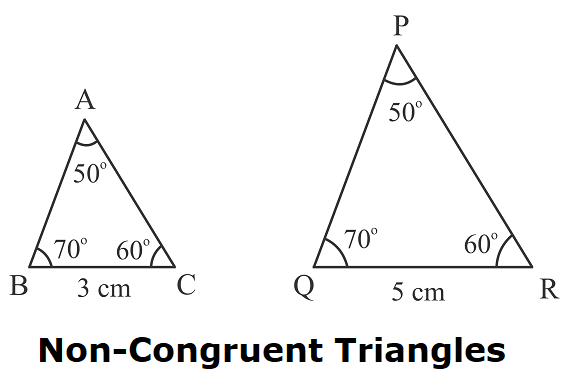
Congruence is an important concept in geometry, and it has many applications in other areas of mathematics, science and engineering. It is used in solving problems and making predictions in fields such as physics, computer graphics, and computer vision.
Leave a Comment